抛物线的图像和性质(抛物线的一些有趣的性质)
抛物线的一些有趣的性质
二次函数的图象抛物线有很多神奇的性质,本篇给出初中解阶段可以理解,可以证明并且有一定应用的四个性质。
1、抛物线平行弦的中点横坐标相同。
先请看下图的动态证明
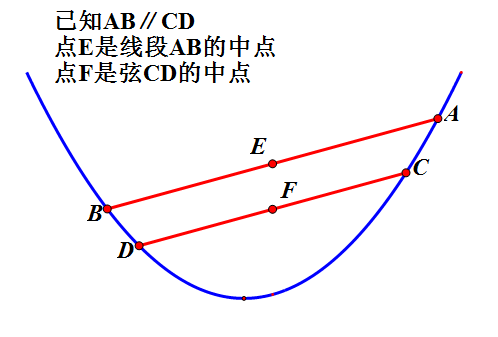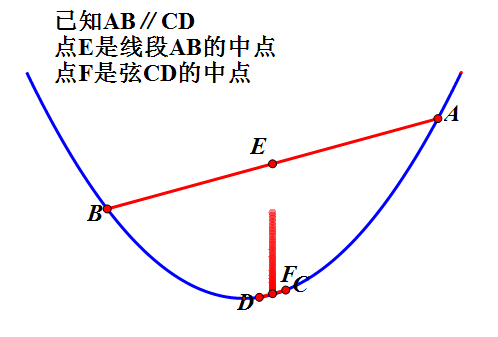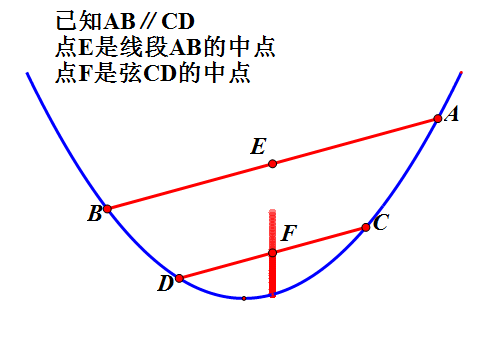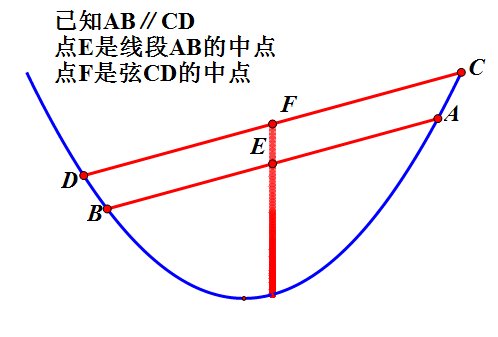

这个性质在咱们解三角形面积最大值的题型中可用于快速得到答案。如下题下图。
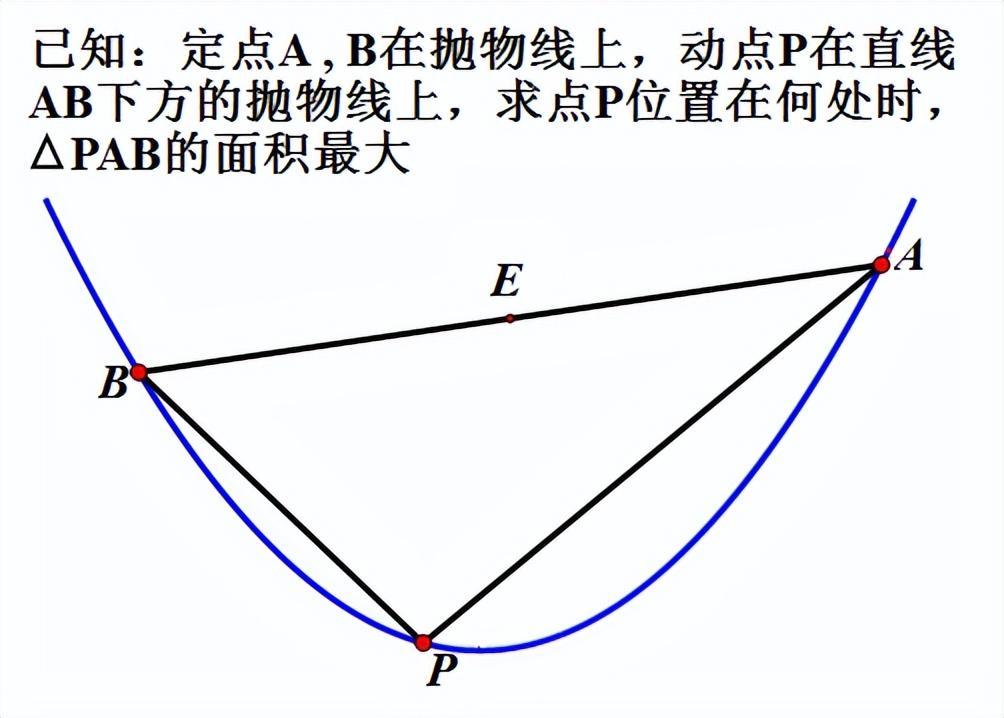
当点P移动到与点A重合时,三角形PAB的面积为零;
当点P移动到与点B重合时,三角形PAB的面积为零;
三角形PAB的面积表达式应该是个二次函数;
二次函数图象有对称性;
你能猜想当点P运动到那个位置时,三角形PAB有最大面积了吗?
大胆猜想,小心求证!
下图给出动态证明(如图动态图不动,耐心等网络传输一会儿数据)
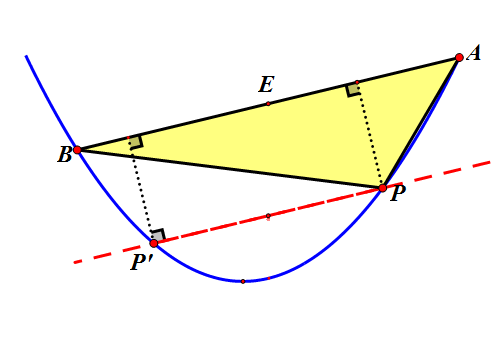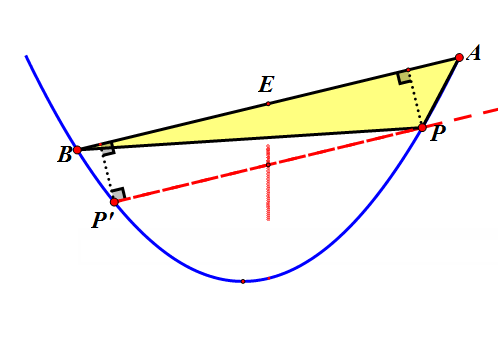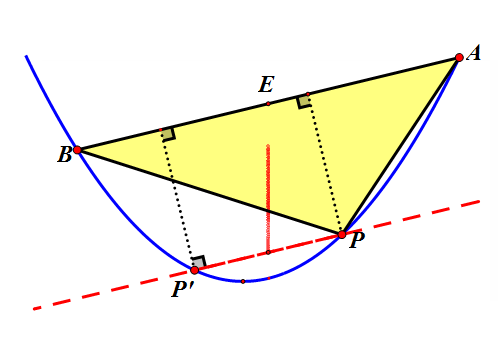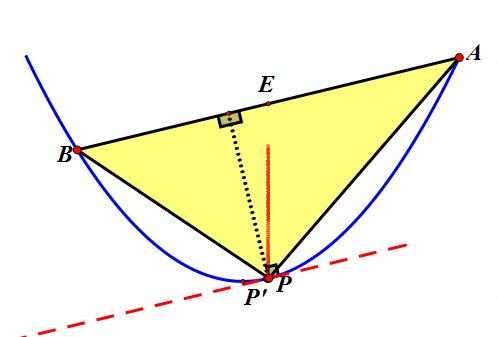
如上图,以AB边为底,过点P作直线PP'∥AB,两条平行线间的距离就是三角形PAB的高,当直线PP'和抛物线相切时,高有最大值,即三角形PAB面积有最大值。此时,弦PP'的中点恰好与点P和点P'重合。
所以,
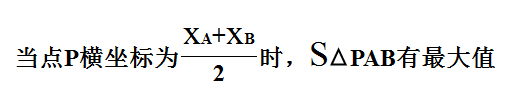
估计有同学会说:“老师,你不讲武德啊,你不是一直让我们用铅锤高与水平宽积的一半求三角形面积吗?咋又变了呢?”
这个方法不是让同学们在试卷上写解题过程用的,因为推理过程太多了,这个方法是让你快速口算检验铅锤高水平宽的方法有无计算失误的。当然填空选择题可以直接用此结论。
而且此方法与铅锤高水平宽法是相通的,请看下面推理

练习:
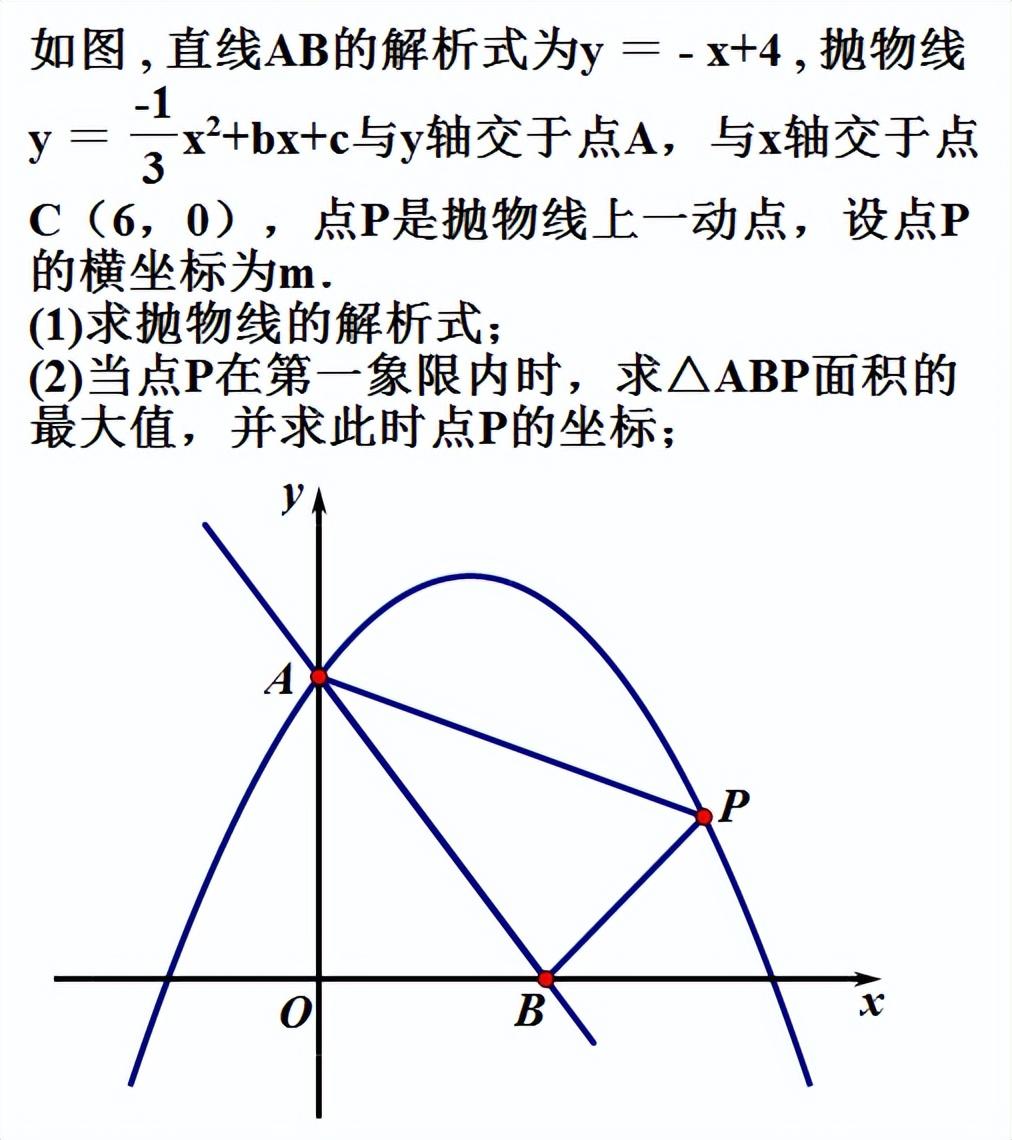
这个练习难度稍大,求三角形面积还能用铅锤高水平宽吗?还能用平行弦的中点横坐标求面积的最大值吗?
请同学们独立思考,动手写一写。答案在本篇最后一行
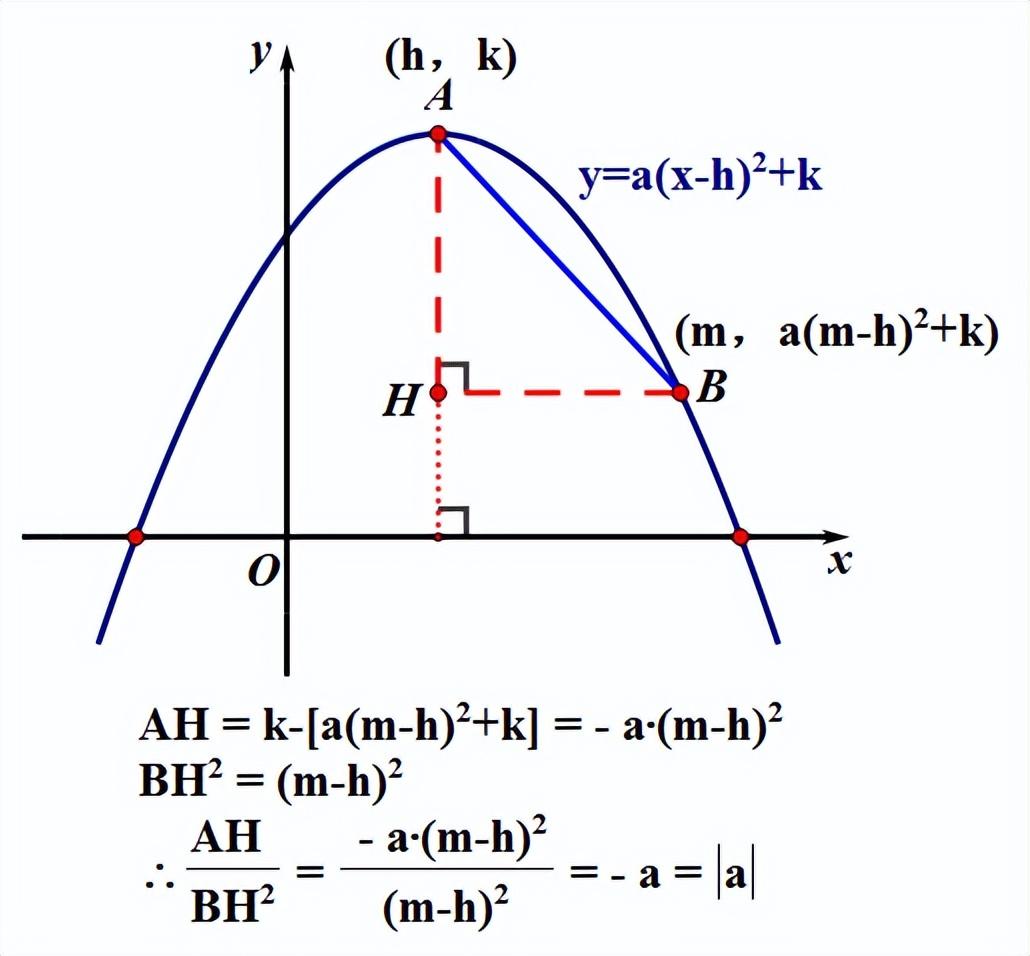
2、抛物线上任意一点与顶点连接,所得线段的铅锤高与水平宽的平方的比为定值。
如下图,我们已经熟知,也无数次用过这个结论。直线上任意两点的连线段,所对应的铅锤高与水平宽的比是定值,这个定值就是斜率k的绝对值。
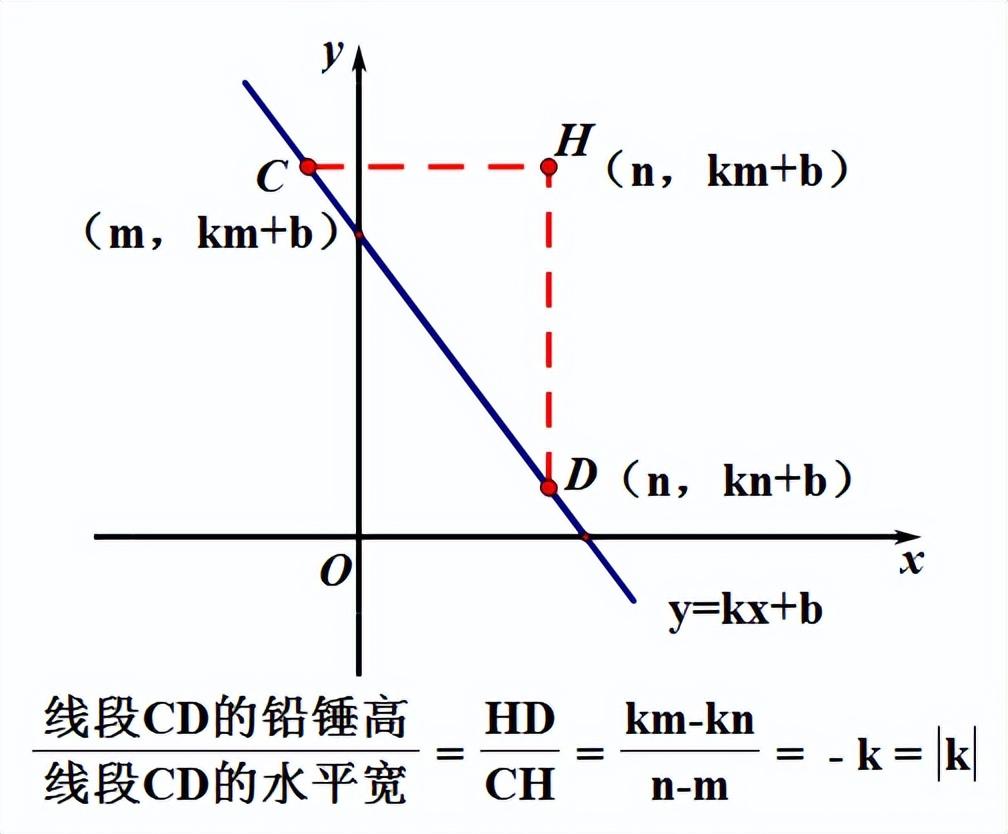
抛物线上也有类似的结论,如下图
例题:
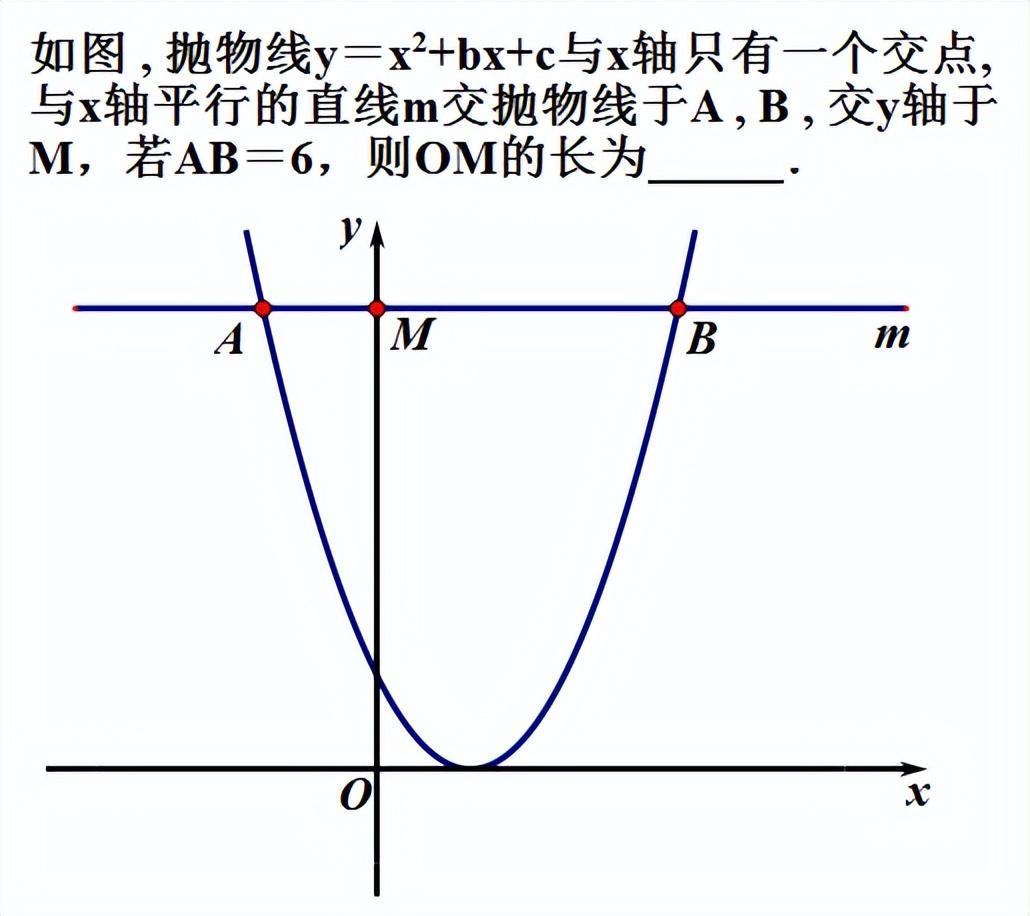
如用常规方法,则此题过程较多,难度较大,如用上面的结论,则可迅速得到答案,OM=9
3、任意两条抛物线是都相似
是的,你没有看错,我第一看到这个结论也以为眼睛欺骗了我。请先看下面的网络上给出的位似定义,再看我根据定义给出的证明。

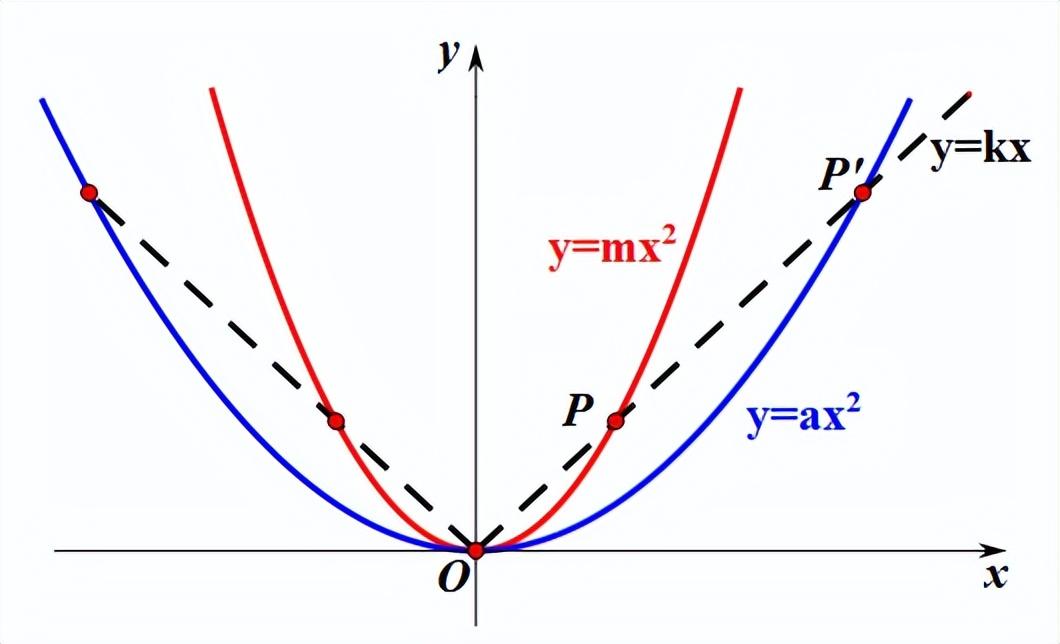

如下图,这样画,是不是更象是位似了

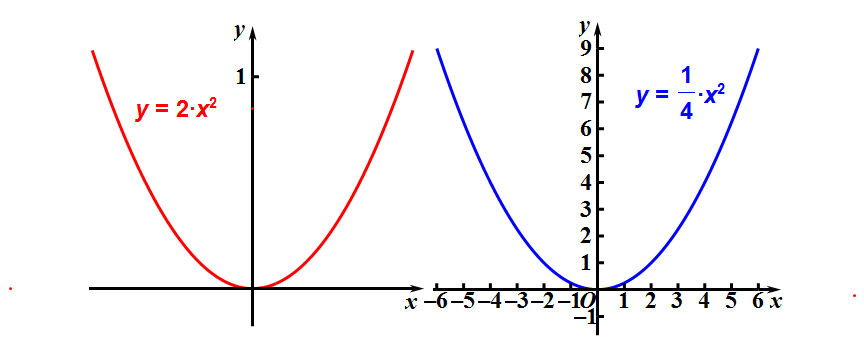
看下面的两个能相互重合的抛物线,它们的解析式不同。
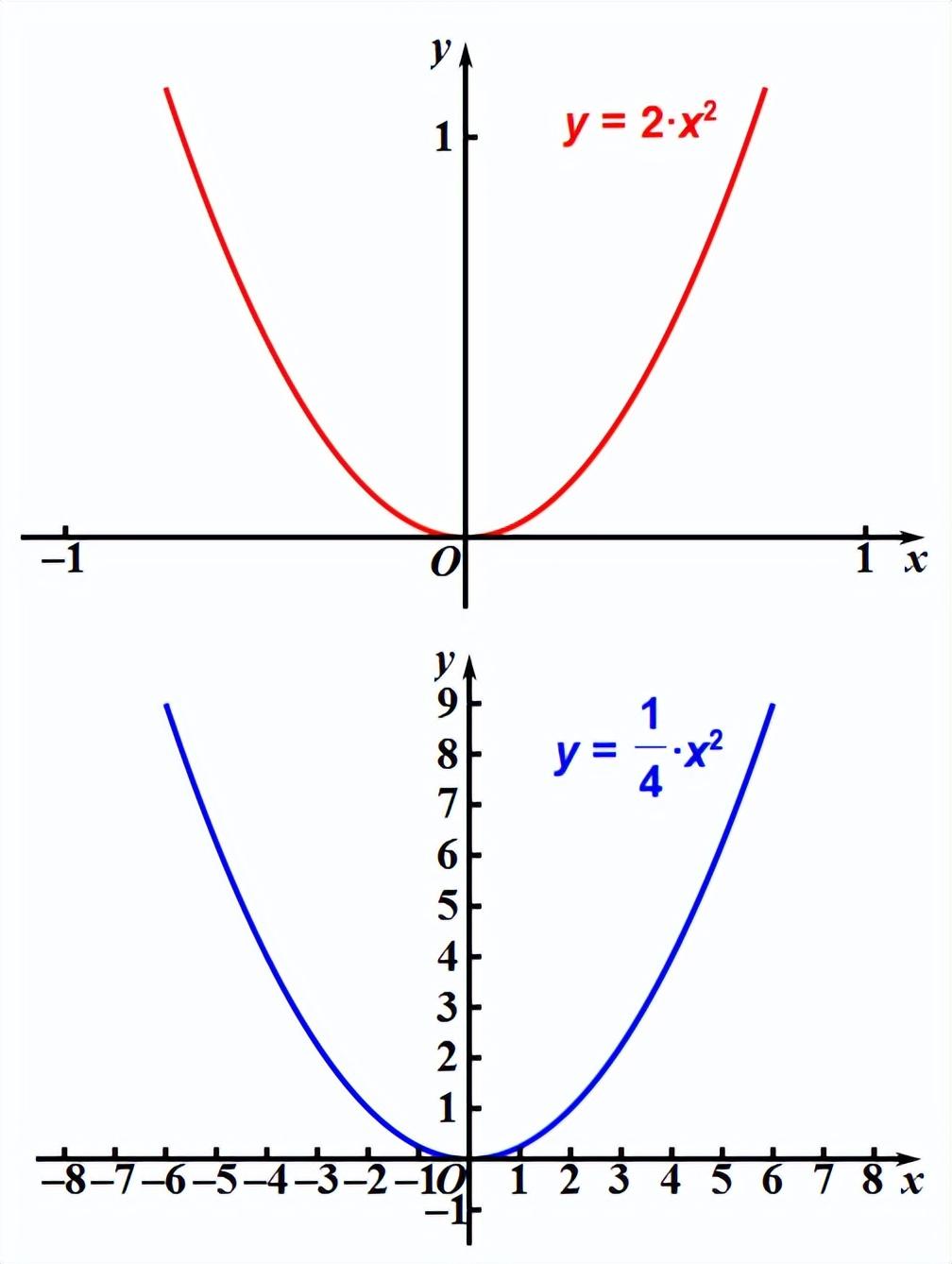
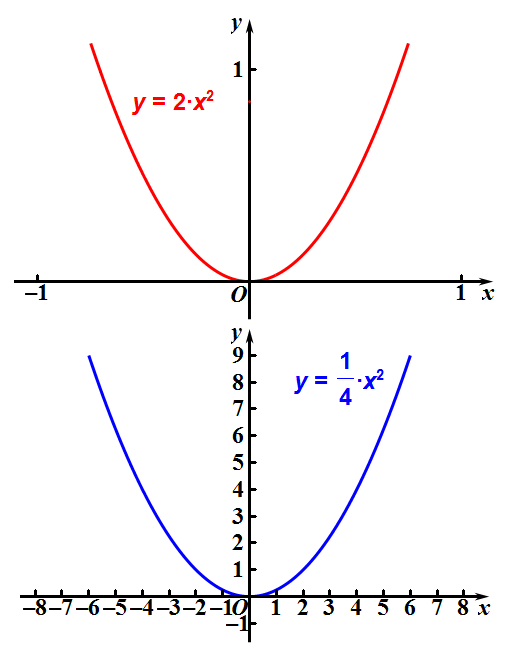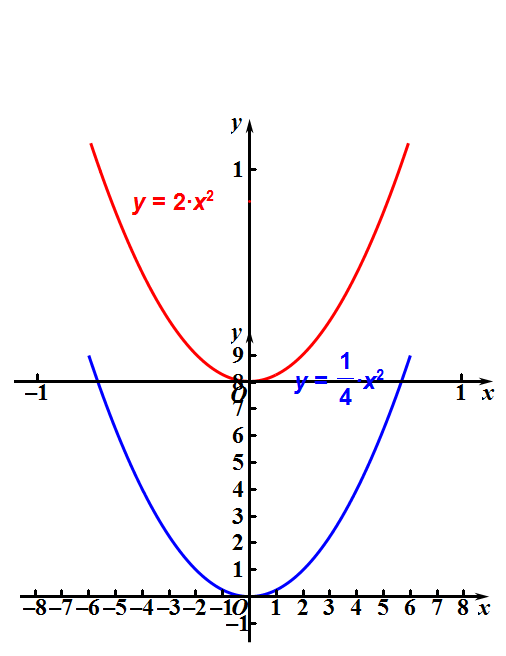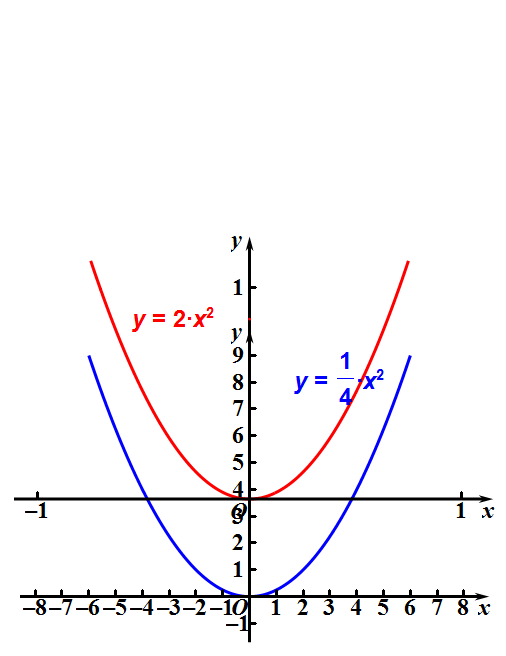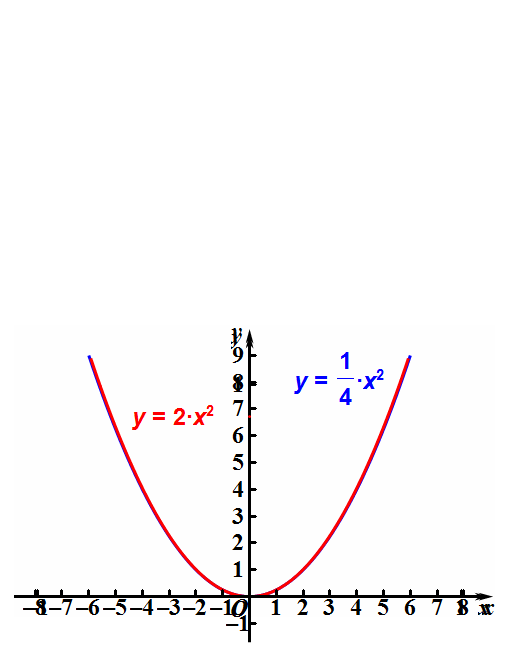
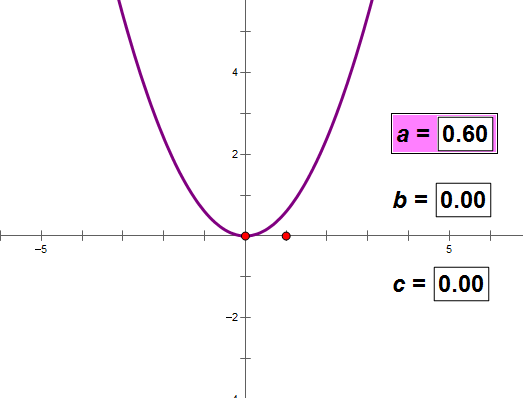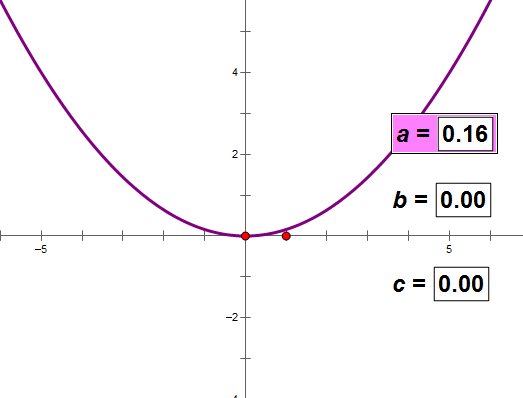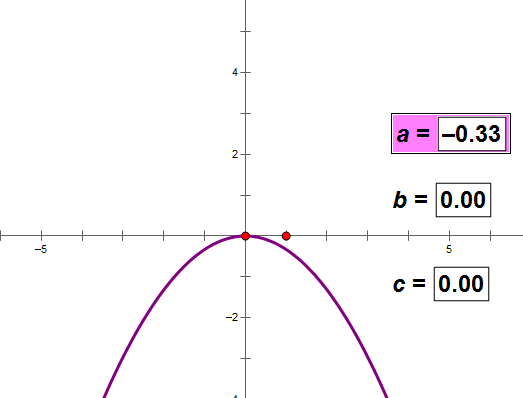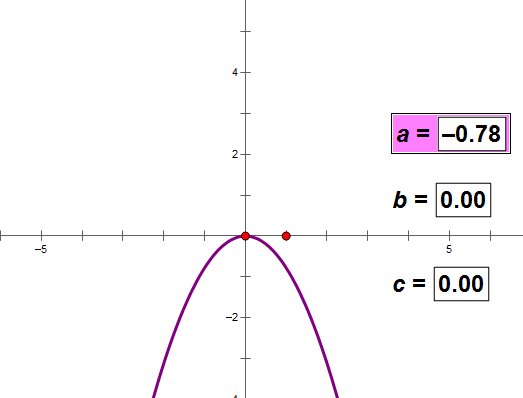
4、抛物线的一般式
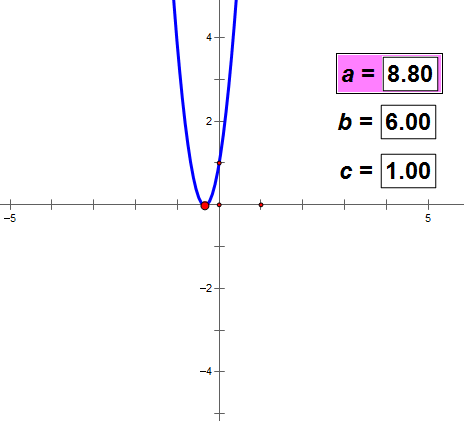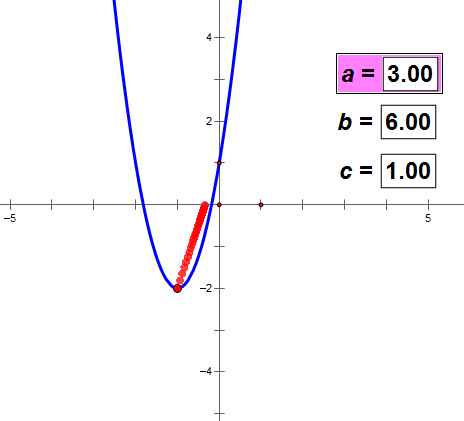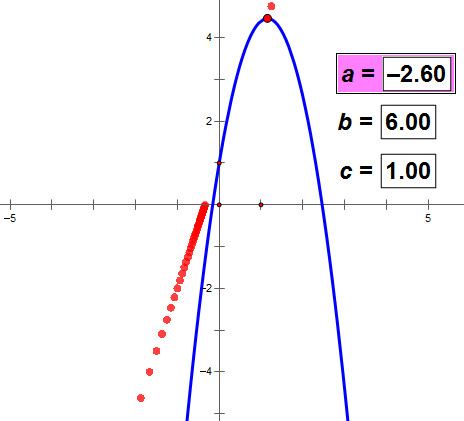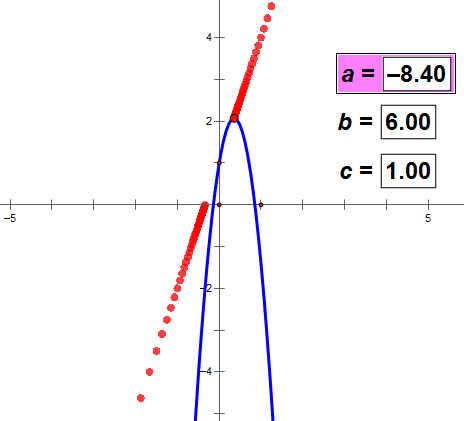
a决定图象的开口方向和顶点的位置,在某种条件下跟开口大小没关系(如上图);
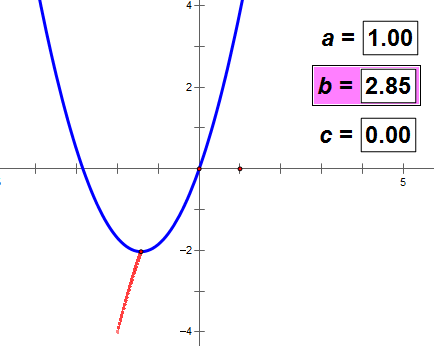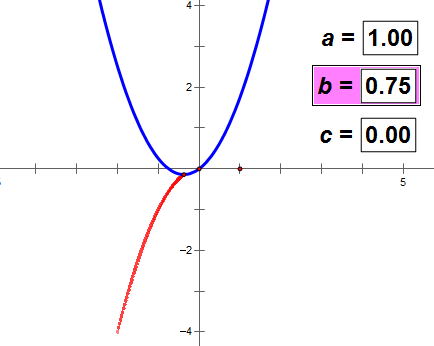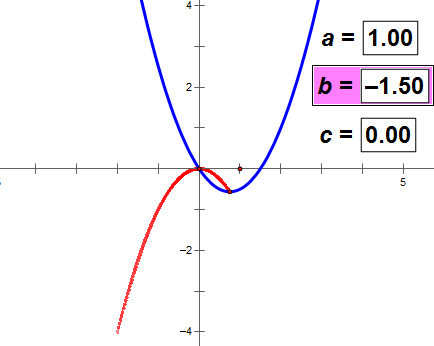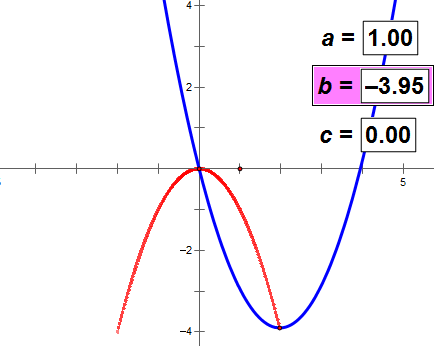
b的值变化,a和c的值不变,则抛物线的顶点轨迹与抛物线成镜面反射;
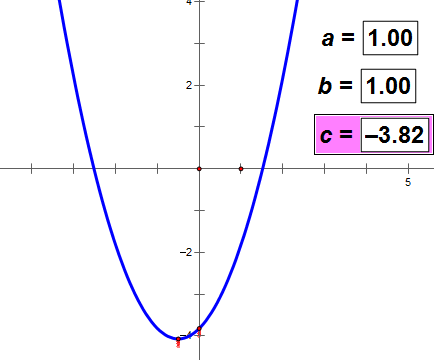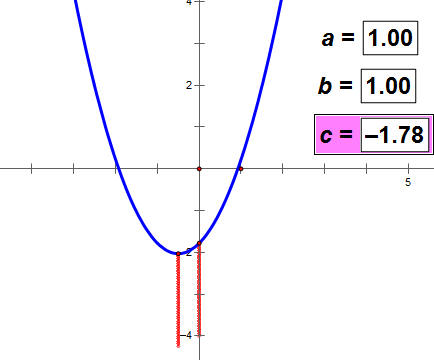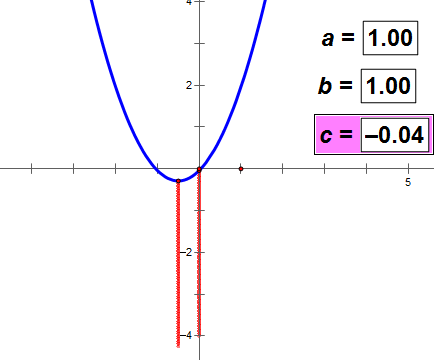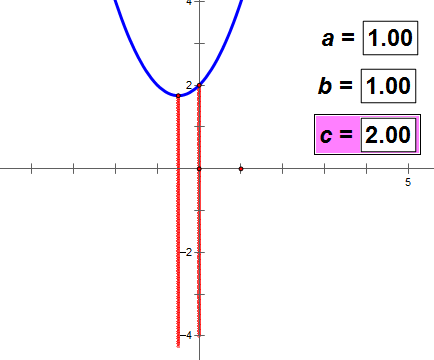
c的值决定抛物线和y轴交点的位置。
没有证明,请看下面的动态图。可以得出上述结论。
(如图动态图不动,耐心等网络传输一会儿数据)
答案:当P点横坐标为4时,三角形ABP的面积最大是8






